Dette på dansk
Random movement of particle in space.
Several years ago I heard about quantum fluctuations in empty space ..
>> According to the theory, there is not a completely empty space in the universe, even if there are no atoms in it. Tiny, extremely volatile so-called subatomic or virtual particles can spontaneously form and disappear again out of the blue as a result of what is called a quantum fluctuation <<
Before that I had heard of Brownian movements:
>> Brownian movements of small particles take place in both liquids and gases. The reason for the movements is the "push" of the molecules which is not evenly distributed on all sides of the particles. The propulsion thus constantly changes direction and size and the paths of motion of the particles on the water therefore become random. <<
I would then find a function that could describe the motion of a particle when it was affected by random quantum fluctuations in empty space.
The movement of a particle that takes place frictionlessly by means of continuous small shocks will, on average, increase the speed away from the starting point
-
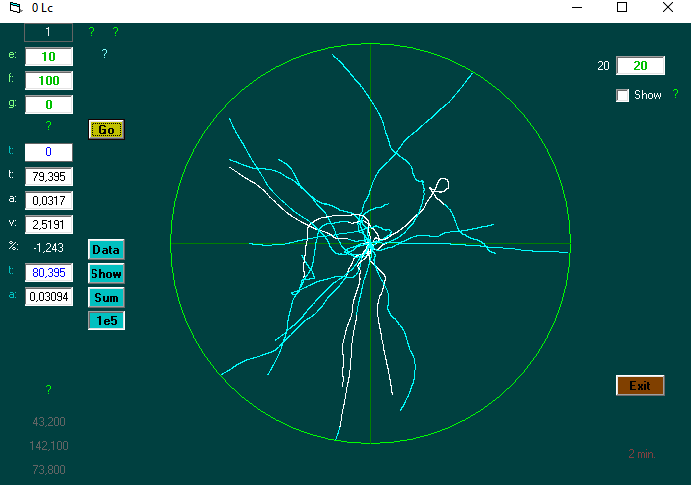
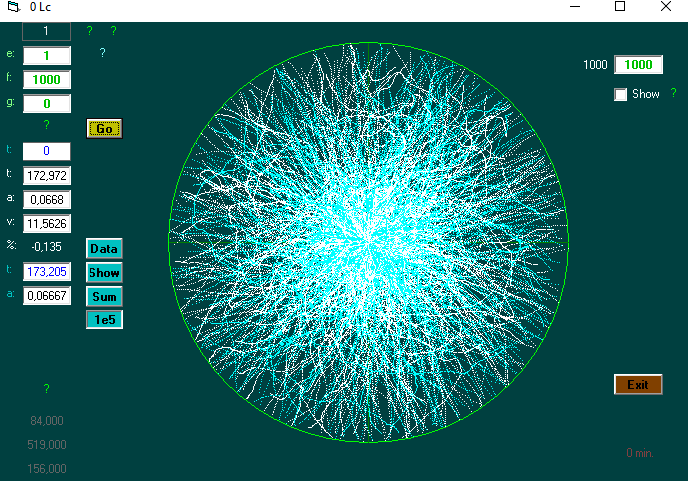
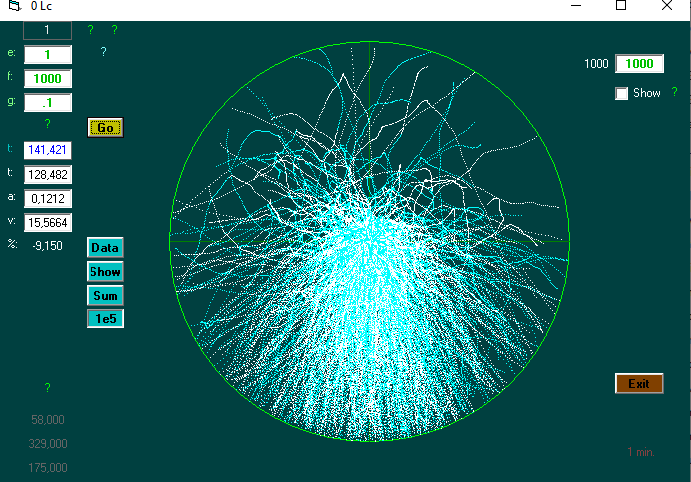
I could not find anything that I could use; so I (am a programmer) developed a computer program that could simulate random motion in empty space (random walk 3d. with drift)
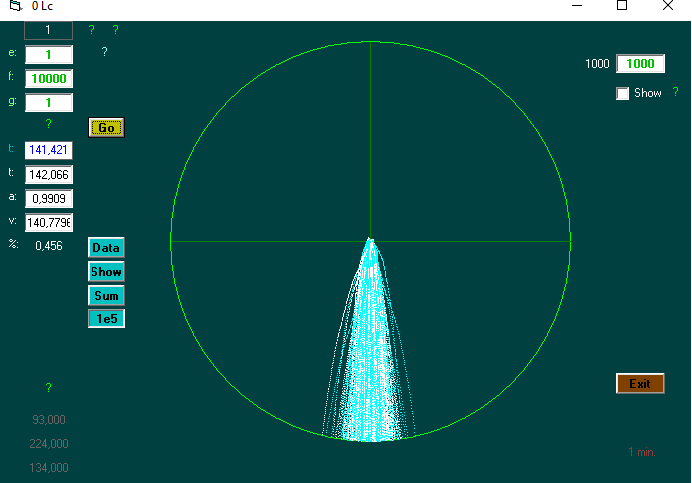
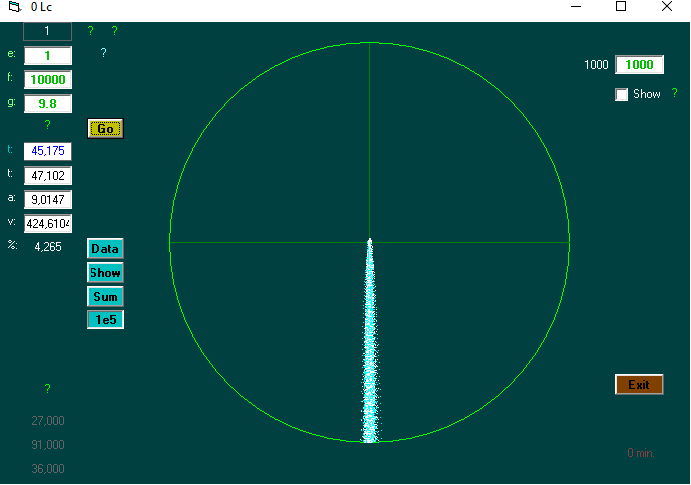
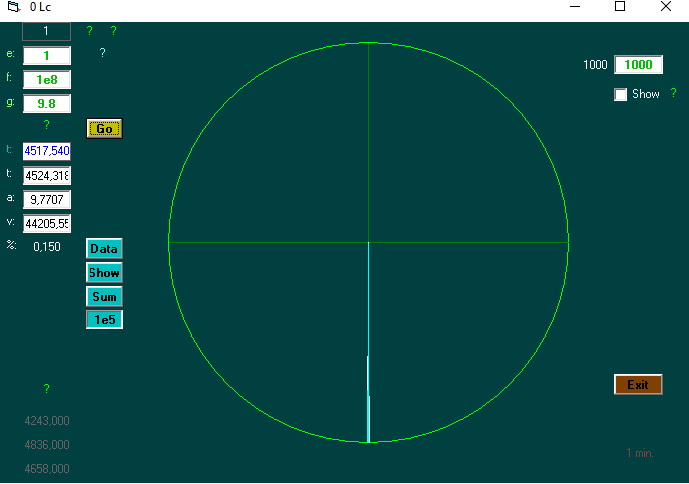
The program can find the time required on average to reach a certain distance. On eg 10,000 tests.
It also shows the path (s) to the given distance ..
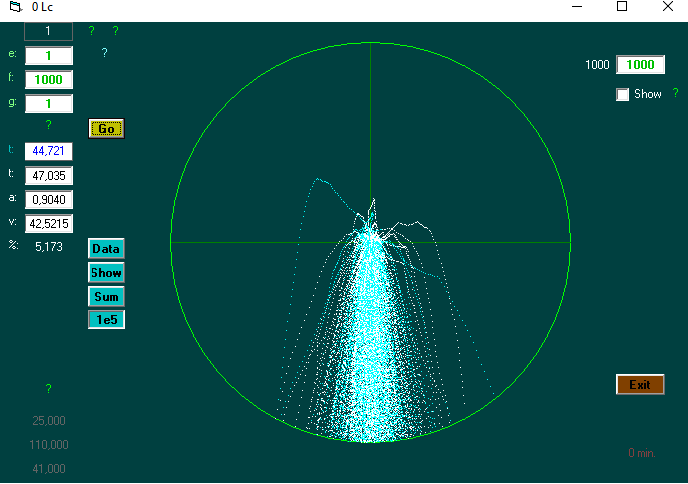
(when g * 6 is inserted in the program when "downward direction" appears randomly, the result will match Newton's law of gravity!)
-
What I am looking for is a function for random walk in space in 3 dim. , where the achieved speed and direction is maintained for the next step. (each step gets a small push with the same force in one of six random directions)
I have searched and searched for a solution - some say it is easy .. but no result yet.
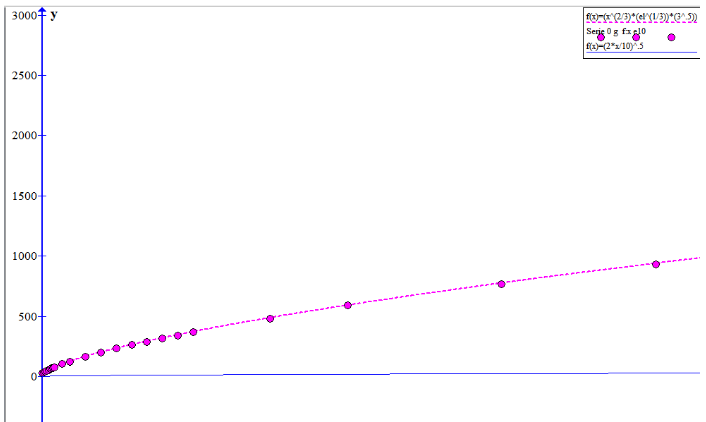
Using countless simulations, I have found (empirically?) A function that can be used; see below.
The challenge:
To develop a mathematical function that gives the average time of a particle moving a given distance in a frictionless space.
And is it possible .. (maybe an answer?)
How does the computer program work?
Enter (e), distance (f), and g.
There are three functions that are held up against the time found. Here f = distance.
Newton's law of gravity: if g is> 0: ((2 * f) / g) ^ 0.5
Georgs 3 d. Random function: if g = 0 and m. Operation: (e ^ (1/3)) * (f ^ (2/3)) * (3 ^ (0.5)) (here: e = 1 (e = elements in a group))
(Found in countless simulations. Is a mathematical model possible ??)
Ordinary random walk: if g = 0 and u. operation: (f) ^ 2
---
Find the number of steps for a distance of x number of meters . (Here is the x radius of a spherical shell.)
1 step of 1 st in 1 sec. - then time = step number
Then check Time against calculated time and deviation percentage can be displayed.
Hypothesis: The quantum fluctuations of the vacuum can affect a lot of particle.
Give the little push in different directions.
It all happens at unimaginable speeds and with unbelievably small fluctuations.
Planck time (5.39 × 10−44 s) is the time it takes for light (300,000 km / s) to move one Planck length (1.6 × 10-35 meters).
---
Time: (1 step of 1 m in 1 sec.) (Step length may vary if it is random)
Time and length do not have to be m and sec.
Program code: (a small part):
.
(enter f (test distance), g and the number of tests)
.
.
.
.
.
.
Let Del = 1: Let Del1 = Del
Again:
Direction = Int ((Rnd * 6) + 1) 'select a random number between 1 and 6 (3 d)
If Direction = 3 Then Del1 = Del1 + (g * 6 * Del) 'downwards; g is entered
Slight R (Direction) = R (Direction) + Part1 * Divide 'movement in time (s * t) (accumulate)
Easy Time = Time + Del '(number of steps)
-
Let X = X + ((R (1) - R (2))))
Let Y = Y + ((R (3) - R (4)))
Let Z = Z + ((R (5) - R (6)))
Plot a pixel on the screen 'to follow developments. At the relative position:
Let position = ((X * X) + (Y * Y) + (Z * Z)) ^ 0.5
'(X and Y are used for plot. Z gives color, inward: blue, outward: white)
-
if position> = the entered distance then exit ..
otherwise Again: etc ..
-
Sum time / test count is result.
Calculate% of the calculated value.
.
.
.
.
Another way to see the challenge--
An imaginary example with a small rocket in space (without g) that is fired continuously once a second, in one of 6 different directions up or down or to the right or left or outwards or inwards - once per second.
Each time the rocket is pushed in one random direction so that it flies at (+/-) 1 meter per second.
If it only got a push, it will continue to fly at 1m / sec
If in the first 3 sec it gets 3 pushes in the same direction, it flies at 3m / sec.
If in the 4th sec it gets a push in the opposite direction, it flies at 2m / sec. etc.
So the question is, how long (how many steps) will it take to reach x meters away on average?
This post has recently (partially) been posted on the website forum.webmatematik.dk under "Hjernevridere", - and although many more than 1000 posts, No function yet ..
(a new quantum gravity law (;-))
Kind regards
Georg
If you should be interested in downloading ( Windows pc ) the simulation-application with random walk 3d for
calculation of time over distances and with variable g –
please refer to:
Group Rnd
If your supplier /Tech Giants/browser/security does not allow for you to download from the site: Please drop me an email and we will sort it out.
Inquiries regarding program download: ggs@skaerbye.com
..