This in English
Tilfældig bevægelse af partikel i rummet.
For flere år siden hørte jeg om kvantefluktationer i det tomme rum..
>> Ifølge teorien findes der ude i universet reelt slet ikke fuldstændig tomt rum, også selv om der ikke findes atomer i det. Bittesmå, uhyre flygtige såkaldte subatomare eller virtuelle partikler kan nemlig spontant dannes og forsvinde igen ud af det blå som følge af det, man kalder en kvantefluktuatio <<
Før det havde jeg hørt om Brownske bevægelser:
>> Brownske bevægelser af små partikler foregår både i væsker og gasser. Årsagen til bevægelserne er molekylernes "skubben" som ikke er ligeligt fordelt på alle sider af partiklerne. Fremdriften ændrer dermed hele tiden retning og størrelse og partiklernes bevægelsesbaner på vandet bliver derfor tilfældige. <<
Jeg ville da finde en funktion, der kunne beskrive en partikels bevægelse, når den blev påvirket af tilfældige kvantefluktationer i det tomme rum.
En partikels bevægelse, der foregår friktionsfrit v.h.a. kontinuerlige små stød vil i gennemsnit forøge hastigheden væk fra udgangspunkt.
--
Jeg kunne ikke finde noget, som jeg kunne bruge; så jeg (er programmør) udviklede et computerprogram, der kunne simulere tilfældig bevægelse i det tomme rum ( random walk 3d. with drift )
Programmet kan finde tiden, som i gennemsnit er nødvendig for at nå en bestemt afstand. På fx 10000 tests.
Det viser også vejen(e) til den givne afstand..
(når der i programmet indsættes g*6 når "retning nedad" tilfældigt fremkommer, så vil resultat matche Newtons gravitationslov!)
--
Det jeg eftersøger, er en funktion for random walk i rummet i 3 dim., hvor den opnåede hastighed og retning bibeholdes for næste step. (hvert step får et lille puf med samme kraft i een af seks random retninger)
Jeg har ledt og ledt - nogle siger, at det er nemt.. men de kommer ikke med en løsning..
Ved hjælp af utallige simuleringer har jeg fundet (empirisk?) en funktion, som kan benyttes; se nedenfor.
Udfordringen:
At udvikle en matematisk funktion, der giver gennemsnitstiden for en partikel, som bevæger sig en given afstand i et friktionløst rum.
Og kan det lade sig gøre.. (måske et svar?)
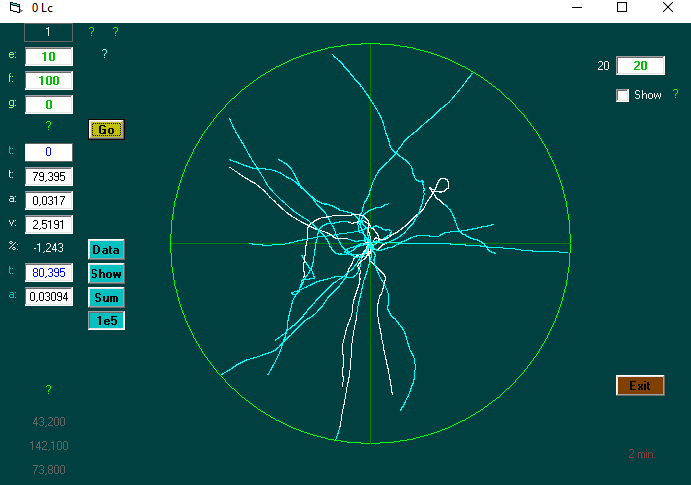
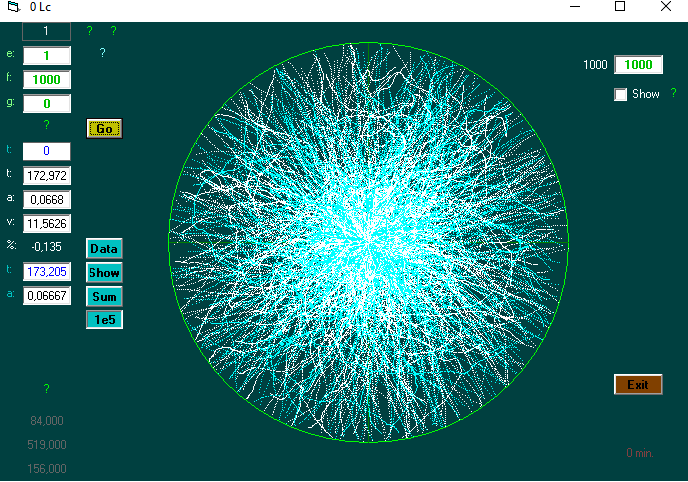
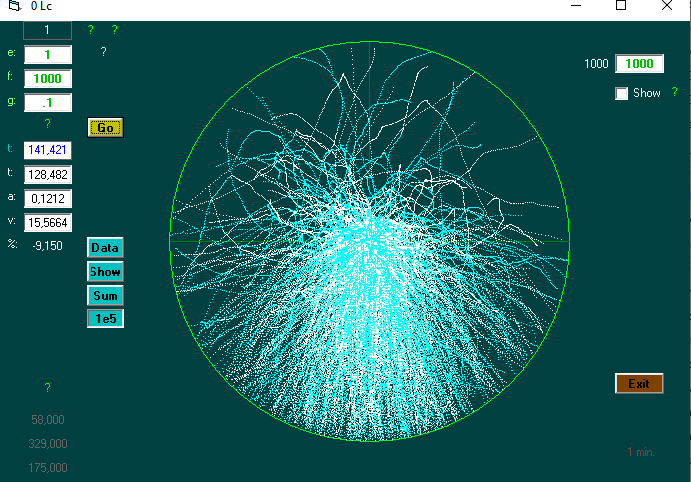
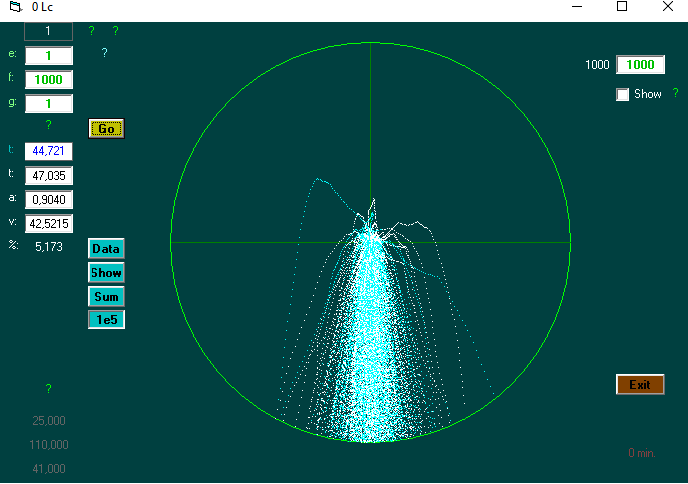
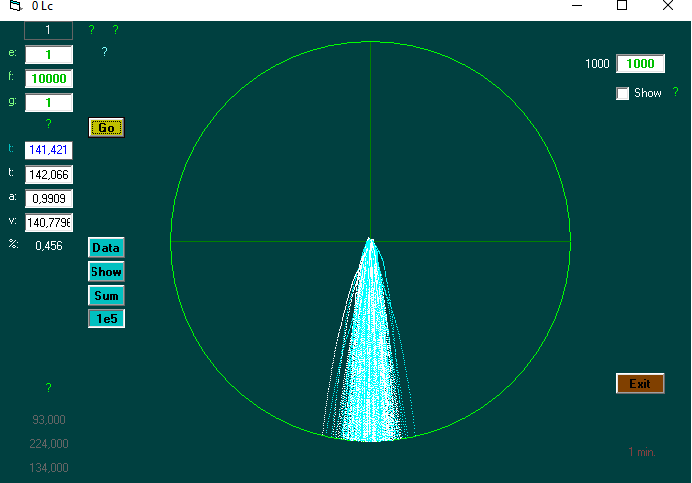
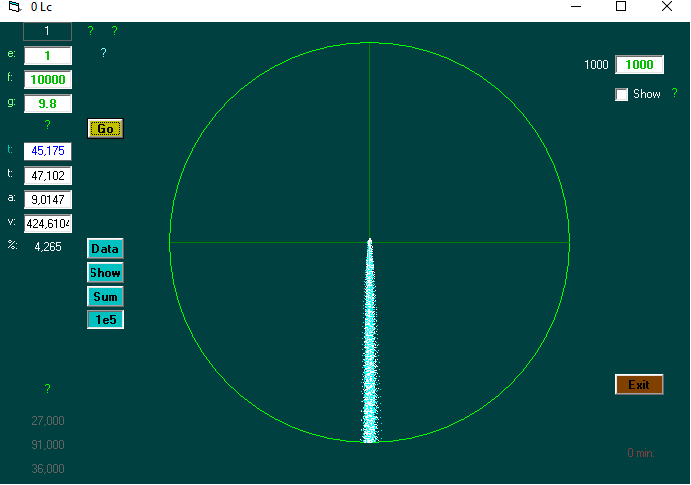
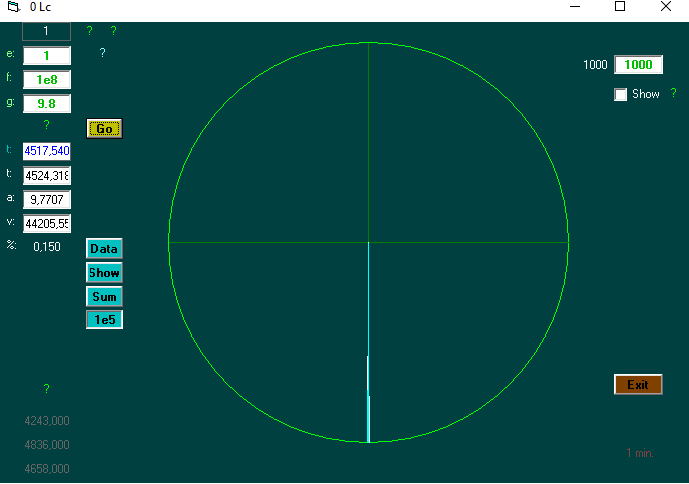
Hvordan virker computerprogrammet?
Der indtastes (e), afstand (f), og g.
Der er tre funktioner, der holdes op imod den fundne tid. Her f=afstand.
Newtons gravitationslov : hvis g er >0 : ((2*f)/g)^0.5
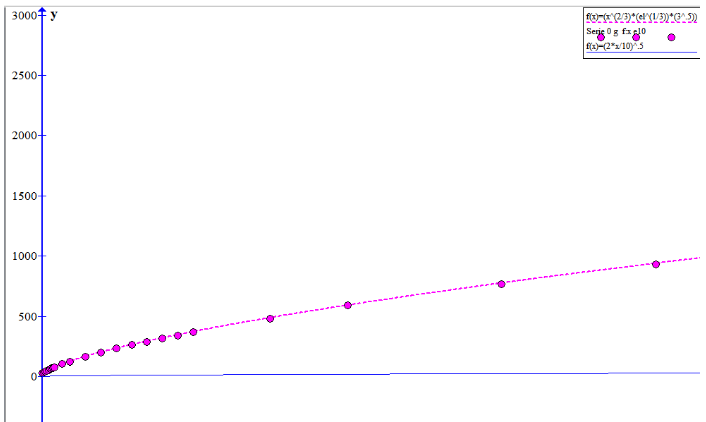
Georgs 3 d. random funktion : hvis g =0 og m. drift : (e^(1/3)) * (f^(2/3)) * (3^(0.5)) (her: e = 1 (e = elementer i en gruppe))
(Fundet ved utallige simuleringer.)
Alm. random walk : hvis g =0 og u. drift : (f)^2
---
Find antal step for en afstand på x antal meter. (Her er x radius for en kugleskal .)
1 step af 1 m på 1 sek. - så er tid = step-antal
Så checkes Tid imod beregnet tid og afvigelse procent kan vises.
Hypotese: vakuummets kvante-fluktuationer kan påvirke en masse partikel.
Give den små puf i forskellige retninger.
Det hele foregår med ufattelige hastigheder og med ufattelige små udsving.
Planck-tid (5,39 × 10−44 s) er den tid det tager for lys (300.000 km/s) at bevæge sig én Planck-længde (1,6 × 10-35 meter).
---
Tid:(1 step af 1 m på 1 sek.) (Step længde må gerne variere, hvis den er tilfældig)
Tid og længde behøver ikke at være m og sek.
Program kode: (en lille del):
.
( indtast f (test-afstand), g og antallet af tests)
.
.
.
.
.
.
Let Del=1:Let Del1=Del
Igen:
Retning = Int((Rnd * 6) + 1) 'vælg et tilfældigt tal mellem 1 og 6 (3 d)
If Retning = 3 Then Del1 = Del1 + (g * 6 * Del) 'nedad; g er indtastet
Let R(Retning) = R(Retning) + Del1 * Del 'bevægelse i tiden (s*t) (akkumulere)
Let Tid = Tid + Del '(antal step)
--
Let X = X + ((R(1) - R(2)))
Let Y = Y + ((R(3) - R(4)))
Let Z = Z + ((R(5) - R(6)))
Plot en pixel på skærmen ' for at følge udviklingen. På den relative position:
Let position=((X * X) + (Y * Y) + (Z * Z)) ^ 0.5
'( X og Y benyttes til plot. Z giver farve, indad: blå, udad: hvid)
--
if position >= den indtastede afstand så afslut..
ellers Igen: osv..
--
Summeret tid/test-antal er resultat.
Beregn % af den beregnede værdi.
.
.
.
.
En anden måde at se udfordringen på--
Et tænkt eksempel med en lille raket i rummet (uden g), der kontinuerligt affyres een gang i sekundet, i en af 6 forskellige retninger op eller ned eller til højre eller venstre eller udad eller indad - een gang pr sek.
Raketten får hver gang et puf i een tilfældig retning så den flyver med (+/-) 1 meter pr sek.
Hvis den kun fik et puf bliver den ved med at flyve med 1m/sek
Hvis den på de første 3 sek får 3 puf i samme retning flyver den med 3m/sek.
Hvis den i 4. sek får et et puf i modsat retning flyver den med 2m/sek. osv.
Så er spørgsmålet, hvor lang tid (hvor mange step) vil den være om i gennemsnit at nå x meter væk?
Dette skriv er for nyligt (delvist) lagt op på hjemmesiden forum.webmatematik.dk under "Hjernevridere" , - og selvom mange flere end 1000 opslag, Ingen funktion endnu..
(en ny kvantetyngdelov (;-))
Mvh.
Georg
Henvendelse ang. program download kan sendes til ggs@skaerbye.com (skriv Random i Emnefelt)
Hvis du vil hente simulations-programmet med random walk 3d til tidsberegning af afstande og med forskellig g,
så kan det hentes via dette link:Group Rnd
Hvis din udbyder/Tech Giants/browser/security ikke lader dig hente/udføre det, kan du sende en e-mail, så kan vi klare det med posten..